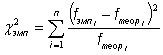Щербатых Сергей Викторович  

кандидат педагогических наук, доцент кафедры математического анализа и элементарной математики, Елецкий государственный университет им. И.А. Бунина, г. Елец

shcherserg@mail.ru
 

Реализация метода математического моделирования в процессе обучения стохастике учащихся профильных классов
 

Аннотация
Статья посвящена проблеме реализации метода математического моделирования при обучении новому компоненту школьного математического образования – стохастике в профильных классах. 

 

Ключевые слова
математическое моделирование, стохастика, профильное обучение

 

Потребность в использовании практических материалов при обучении стохастике в общеобразовательной школе определяется тем, что возникновение, формирование и развитие основных стохастических понятий и идей имеют своим источником чисто человеческие ощущения и восприятия. Одним из наиболее плодотворных методов стохастического познания окружающей действительности является метод построения математических моделей.

Наиболее рациональным определением «модели» с точек зрения педагогики и психологии математики является определение, предложенное Л.М. Фридманом: «моделью некоторого объекта (прототипа) называется такой естественный или искусственный объект, который в определённом отношении подобен прототипу (оригиналу), используемому в качестве заместителя прототипа, и изучение которого даёт новые знания о прототипе» [1, с. 54].

Среди множества всевозможных моделей особую роль играют математические модели. Так, по Р.С. Черкасову и А.А. Столяру, «математическая модель – это приближённое описание какого-нибудь класса явлений, выраженное на языке какой-нибудь математической теории, с помощью системы алгебраических уравнений или неравенств, дифференциальных или интегральных уравнений, функций, системы геометрических предложений или других математических объектов» [2, с. 144].

Использование моделирования в обучении имеет два аспекта. Во-первых, моделирование является тем особым содержанием, которое должно быть усвоено в результате обучения методом познания, и, во-вторых, моделирование является той учебной деятельностью и средством, без которого невозможно полноценное обучение [3].

Специфической особенностью стохастики является тот факт, что она более других математических разделов связана с действительностью, т.е. границы реальных объектов и их моделей весьма размыты. Поэтому, с одной стороны, мы должны акцентировать внимание учащихся профильных классов на данное обстоятельство, а с другой стороны, обучение должно быть построено так, чтобы старшеклассники умели отличать реальные объекты от их моделей. Обучение науке о случайном должно в какой-то мере имитировать описанный процесс исследования на практике, раскрывать связи математики с реальным миром, с другими областями знаний, в которых она находит всё новые и новые приложения. Поэтому обучение должно начинаться с рассмотрения реальных ситуаций, производственных процессов и возникающих в них задач, с поиска средств для их математического описания, построения соответствующих математических моделей. Затем объектом изучения должны стать уже сами эти модели, их исследование, приводящее к расширению теоретических знаний учащихся профильных классов. После того, как соответствующая теория построена (при участии самих учащихся), её аппарат применяется к решению исходной задачи, а также других задач, связанных с другими областями явлений, но приводящих к моделям этого же класса [2].

Придерживаясь мнения авторитетных учёных [4-6], можно сказать, что основу метода математического моделирования составляют следующие этапы процесса математизации:

• этап перехода от ситуации, которую необходимо разрешить, к формальной математической модели этой ситуации, к чётко поставленной математической задаче – этап формализации;

• решение поставленной математической задачи методами, развитыми в самой математике для задач данного типа, составляет содержание второго этапа – этапа решения задачи внутри построенной математической модели;

• интерпретация полученного решения математической задачи, применения этого решения к исходной ситуации и сопоставления его с нею.

Кратко эти три этапа можно назвать этапами:

• построение математической модели;

• получение математических результатов;

• принятие решения (выводы в реальном мире).

Наиболее ответственным и сложным является первый этап. Построение математической модели осуществляется логическим путём на основе глубокого анализа изучаемого явления и требует умения описать явление на языке математики (в частности, стохастики). В процессе построения модели можно выделить несколько шагов.

Первый шаг – индуктивный. Он заключается в отборе наблюдений, относящихся к тому процессу, который предстоит в последующем моделировать. На этом шаге формулируется проблема, то есть принимается решение относительно того, что следует принимать во внимание, а чем можно пренебречь.

Второй шаг заключается в переходе от определения проблемы к построению модели, пусть ещё неформальной. На данном шаге рассматривается ряд наборов неформальных допущений, способных объяснить одни и те же данные. Таким образом, рассматриваются несколько различных моделей и решается, какая из них лучше всего отображает изучаемый процесс.

Третий шаг заключается в переводе полученной, ещё «неформальной» модели в математическую модель, который включает в себя рассмотрение словесного описания «неформальной» модели и поиск подходящей математической структуры. Следует отметить, что это самый сложный этап во всём процессе моделирования. При этом стадия перевода таит в себе ряд опасностей. С одной стороны, сами по себе «неформальные» модели часто неоднозначны, и поэтому существует несколько способов перевода «неформальной» модели в математическую. С другой стороны, язык математики (в частности, стохастики) лишён двусмысленностей и более точен, чем житейский язык. Благодаря ему исследуется скрытый смысл различий в формулировках, который практически недоступен исследованию посредством житейского языка.

Следующий этап – получение математического р     езультата, т.е. решение задачи в рамках математической теории и является решающим в математическом моделировании. На данном этапе применяется весь арсенал стохастических методов с целью формального вывода следствий из исходных допущений модели. На стадии получения математического результата имеют дело с чистыми математическими абстракциями и используют одинаковые математические средства. Данный этап представляет собой дедуктивное ядро процесса математического моделирования.

На последнем этапе полученные в ходе решения выводы проходят через ещё один процесс перевода – с языка чистой стохастики на житейский язык.

Учителю следует добиться от старшеклассников чёткого понимания значения и содержания каждого из выше описанных этапов процесса математического моделирования. Это нужно для того, чтобы учащиеся усвоили, что они решают не просто стохастическую задачу, а конкретную жизненную ситуацию с помощью стохастики. Тогда старшеклассники смогут увидеть в стохастике практическое значение, и не будут воспринимать её как абстрактную и бесполезную науку [7]. В качестве примера рассмотрим задачу.

Задача. При самоопылении гороха, полученного от скрещивания растений с жёлтыми гладкими и зелёными морщинистыми семенами было получено: 876 растений с жёлтыми гладкими, 321 – с жёлтыми морщинистыми, 298 – с зелёными гладкими и 115 – с зелёными морщинистыми семенами. Можно ли утверждать, что подобное расщепление подчиняется 3-му закону Г. Менделя (дигибридное скрещивание)?

Решение. Построение математической модели. Пусть  – количество растений гороха, полученных в опыте и наделённых определённым признаком. Тогда:  – количество растений с жёлтыми гладкими семенами,  – количество растений с жёлтыми морщинистыми семенами,  – количество растений с зелёными гладкими семенами,  – количество растений с зелёными морщинистыми семенами.

Объём выборки равен . Тогда , , , .

Выдвигаем гипотезы:

={данное расщепление – дигибридное с расщеплением 9:3:3:1}; ={расщепление не является дигибридным}.

В качестве критерия значимости выбираем критерий «хи-квадрат» Пирсона: (объём выборки ) – математическая модель рассматриваемой ситуации. Здесь  – предполагаемое количество растений гороха, наделённых определённым признаком и согласующихся с теоретическим распределением.

Получение математических результатов. Для применения данного критерия необходимо рассчитать теоретические частоты (частоты контрольной выборки), согласующиеся с дигибридным скрещиванием. 

Так как , то ; ;

; .

Рассчитаем эмпирическое значение критерия:

.

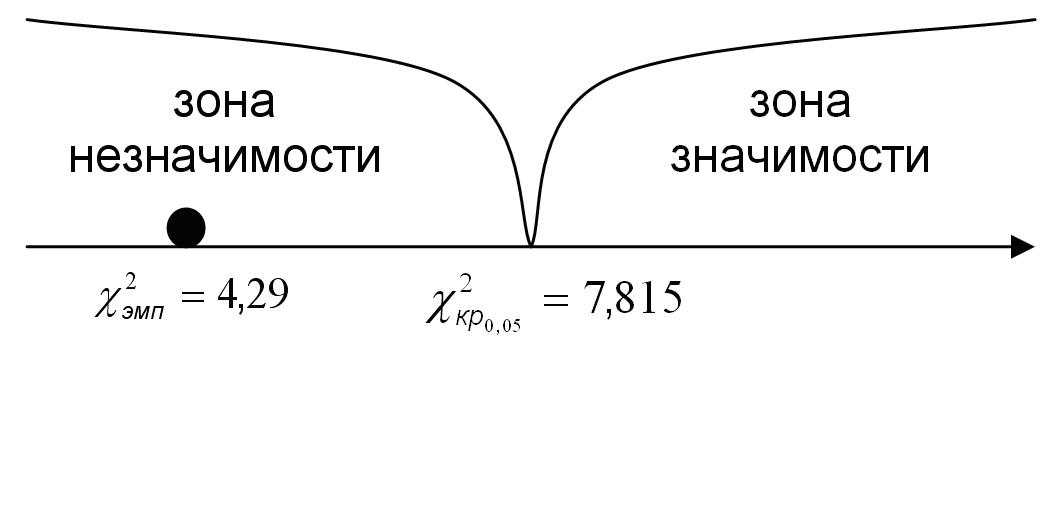
Чтобы найти критическое значение критерия, необходимо знать число «степеней свободы» и уровень значимости. В данной задаче , так как имеем 4 класса-интервала и одно ограничение (объём выборки должен быть равен п). В качестве уровня значимости выберем . По статистической таблице критерия находим критическое значение: . 

Строим «ось значимости»:

В нашем случае  попало в зону незначимости. В соответствии с правилом принятия решения, мы оставляем гипотезу  и отвергаем .

Принятие решения (выводы в реальном мире). При переводе результата, полученного в ходе математических вычислений, заключаем, что данное расщепление в полной мере удовлетворяет 3-му закону Г. Менделя [8].

В непосредственной практике традиционного обучения мир реальных объектов подменяется изучением соответствующих им понятий и других продуктов познания, полученных не учениками, а специалистами, учёными или авторами учебного материала.

Подобное положение усугубляется при изучении основ науки о случайном. К примеру, классическая вероятность, базируемая на гипотезе равновозможности исходов, является математической моделью, отсечённой от этапов формализации и интерпретации. Вычисление вероятностей с помощью комбинаторных правил, их косвенный подсчёт на основе заданных, неизвестно откуда взятых вероятностей – всё это представляет собой оперирование внутри математических моделей.

При таком обучении некоторые понятия (вероятность, математическое ожидание, дисперсия, среднее квадратичное отклонение, функция распределения, плотность, мода, медиана, статистический критерий, коэффициент корреляции и т.п.) воспринимаются как искусственные и инородные по отношению как к самой математике, так и к жизни. Не случайно многие обучаемые испытывают внутреннее психологическое сопротивление этой науке.

Для того, чтобы снять данную проблему, необходимо изменить методологию обучения с помощью первоначального задания ученикам в качестве образовательных объектов реальных, а не идеальных объектов познания [9]. При таком изучении вырабатываются умения решать стохастические задачи, выдвигаемые практикой, что и будет являться критерием достижения поставленных целей.

Резюмируя вышесказанное, следует отметить, что включение математического моделирования в учебный процесс делает его более рациональным и одновременно активизирует познавательную деятельность учащихся профильных классов. Следовательно, на уроке математики осуществляется развитие учащихся. Моделирование отражает теоретический стиль мышления, который содействует развитию учащихся и приобщает их к научному стилю мышления, поэтому понятие математической модели и некоторые общие положения, связанные с ним, должны в той или иной форме иллюстрироваться на протяжении всего периода обучения стохастике в профильных классах.

Литература

1. Фридман Л.М. Сюжетные задачи по математике. История, теория, методика / Л.М. Фридман. – М.: Школьная пресса, 2002. – 208 с.

2. Методика преподавания математики в средней школе: Общая методика: учеб. пособие для студентов пед. ин-тов по спец. 2104 «Математика» и 2105 «Физика» / А.Я. Блох, Е.С. Канин, Н.Г. Килина и др.; сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение, 1985. – 336 с.

3. Морозов Г.М. Методика формирования умений строить математические модели при обучении математике: автореф. дис. … канд. пед. наук. – М.: НИИ СиМО АПН СССР, 1978. – 21 с.

4. Плоцки А. Стохастические задачи и прикладная направленность в обучении математике // Математика в школе. – 1991. – № 3. – С. 69-71.

5. Терешин Н.А. Прикладная направленности школьного курса математики: кн. для учителя / Н.А. Терешин. – М.: Просвещение, 1990. – 96 с.

6. Фирсов В.В. Некоторые проблемы обучения теории вероятностей как прикладной дисциплине: дис. … канд. пед. наук. – М., 1974. – 161 с.

7. Щербатых С.В. Применение математического моделирования в процессе реализации профессионально-прикладной направленности обучения школьников стохастике // Математика в образовании: сб. статей. Вып. 4 / Под ред. И.С. Емельяновой. – Чебоксары: Изд-во Чуваш. ун-та, 2008. – С. 108-110.

8. Щербатых С.В. Статистические гипотезы и способы их проверки // Математика. – 2008. – № 7. – С. 22-27.

9. Селютин В.Д. Научные основы методической готовности учителя математики к обучению школьников стохастике: дис. … докт. пед. наук. – Орёл, 2002. – 344 с.

   Рекомендовано к публикации:
   А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

   -----

Sergey V. Shcherbatykh
Сandidate of Pedagogical Sciences, Associate Professor of the Chair of Mathematical analysis and elementary mathematics, Elets State University, Elets
shcherserg@mail.ru

Realising the method of mathematical modelling in the course of teaching stochastics the pupils of profile classes

The article is devoted to the problem of realizing the method of mathematical modelling while teaching a new component of the school mathematical education – stochastics in profile classes. 

Keywords: mathematical modelling, stochastics, profile training